「三角形の成立条件」をシミュレーション/図解で解説![数学入門]
目次
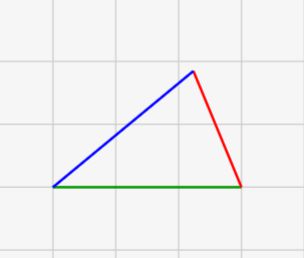
適当な三辺の長さを決めると三角形が出来上がる。けど、常に成立するわけではない><
三角形は3辺の長さが決定されれば、自動的に形が決まります。↓のように、各辺の大きさのバランスによってその形が決まります。
しかし、常にどんな辺の大きさのバランスでも三角形が描けるわけではありません。今回は、そのような「三角形が成立する条件」について詳しく説明します!シミュレーターもあるので、実際に三角形を作ることもできますよ!
三角形の成立条件
それでは三角形が成立する条件を考えてみましょう。
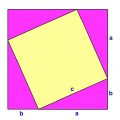
三角形になるためには、「二辺(c,b)の長さの和 > 辺aの長さ」が成立する必要があります。各辺はその他二辺の和より長くてはいけないのです。
そのため、全ての辺において、↓の式が成り立つことが必要条件となります。
以下、各辺の長さをa,b,cとして定式化します。
どの辺も、「その他二辺の和」よりも長くてはいけない
↓
\( \displaystyle a < b + c \)
\( \displaystyle b < a + c \)
\( \displaystyle c < a + b \)
上記式を少し変形すると、↓のような条件に置き換えることもできます。
どの辺も、「その他二辺の差の絶対値」より長くてはいけない
↓
\( \displaystyle |b – c| < a \)
\( \displaystyle |a – c| < b \)
\( \displaystyle |a – b| < c \)
こちらの場合は、二辺の差分値がもう一辺よりも小さくないという条件です。このような条件さえ成立していれば三角形になれるワケです!
三角形が成立するかシミュレーターで実験して理解しよう!
上記のように、三角形が作成できる条件があることを確かめるために、↓のシミュレーションでその制約を確かめてみましょう!
↓の値を変えると、辺の大きさをそれぞれ変えることが出来ます。すると、下図に指定の大きさの三角形が描かれます。色々辺の大きさを変えてみて、どのようなときに三角形が描けなくなるのか確認してみましょう!
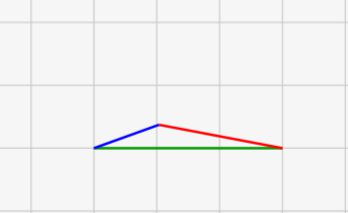
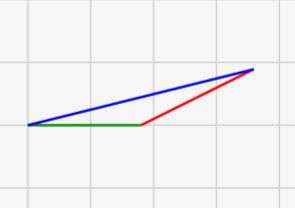
三角形が成立しなくなる直前には、三角形の高さが小さくなり、角度が180度に近づく!
↑のシミュレーターでいくつか辺の長さを変えて実験してみると、三角形が消える直前には↓のような三角形が描かれていることに気がつくと思います。
ほとんど高さがなくなり、真っ平らになっていますね。別の言い方をすると、角度が180度に近づき、底面に近くなっています。
限界点では\(a ≒ b + c\)という式になり、一辺が二辺の長さとほぼ同じ大きさになります。なのでギリギリ三角形が成立してる状態であり、辺aがもう少し長かったら不成立となります。
次回は三角形の面積の公式について確認していきます!
今回は、今後三角形の定理を説明していくために、一番重要な三角形の成立条件について説明しました!今後もこの条件は成立している前提で話していきますので覚えておいて下さい!
次回は今回作ったような三角形における面積の求め方について解説します!
- 3つの辺がなんでも良いわけでなく、三角形には成立条件がある
- 一番長い辺が、他の二辺の長さの和よりも短ければ三角形は成立する
⇒「幾何学・図形」カテゴリ記事一覧
その他関連カテゴリ