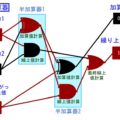
「固定小数点」をシミュレーションで解説![コンピューターの原理基礎]
コンピューターは2進数の世界で動いています。2進数は1001101101みたいな感じで0と1の羅列となってます。
前回までコンピューター内での整数の表現(Int,Long)について説明しました。
今回はさらに細かい数を表すのに必要な「小数」の表現方法について説明します!
![「固定小数点」をシミュレーションで解説![コンピューターの原理基礎]](https://retu27.com/wp-content/uploads/20220228194536-500x224.png)
目次
おさらい:「2進数で整数を表現」
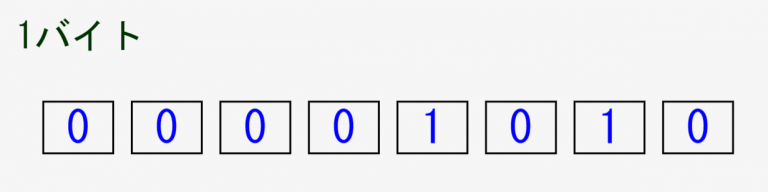
コンピューターは↓のように0 or 1が入る箱(bit)を組み合わせて、それによって数値表現をします。
↓は1バイト(8bit)で、数値としては0~255の256パターンを表現できます!
固定小数点:一番簡単な小数の表現方法
↑のままだと、コンピューターは整数しか表現できません。
そこで、「どこかのbitの区切りに小数点をおくと決めて、それをベースで小数を表す」ことを考えます。
例えば、「右から1つ目のbitの位置に小数点を置く」と決めた例が↓です。本来ならば、00000111は10進数の7なのですが。この例だと3.5になります。なぜなら、小数点の位置が1つズレたため、2進数で「00000011.1」を表すことになるからです!
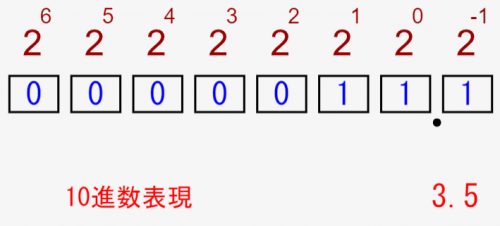
ところで、2進数上の「11.1」って、どのような数字なんでしょうか?
2進数の小数点の各桁は、\(2^{-1},2^{-2}…\)と評価されていく!
2進数上の小数点は↓の注釈があるとおり、\(2^{-1},2^{-2}…\)とマイナス指数で評価されていきます。

コチラの指数の説明ページでも解説していますが、桁が上がると指数は1つ上がるので、桁が下がると指数はマイナスになるんです。そしてマイナスの指数の評価は↓のように2の累乗の逆数になります。
2桁目: \(\large{2^{-2} = \frac{1}{4}}\)
3桁目: \(\large{2^{-3} = \frac{1}{8}}\)
このため、2進数の11.1は↓のような計算になり、10進数でいう3.5と評価できるんです!
\(\large{2^1 + 2^0 + 2^{-1} = 3.5} \)
このように、固定小数点方式では「小数点を決まった位置にズラす」ことで小数を表現するんです!
「固定小数点」をシミュレーターで確認してみよう!
固定小数点でどのように小数が表現できるか、実際にシミュレーターで確認してみましょう!簡単のために1バイトでの固定小数点表現になります。
- 指定した16進数を各bitに代入し、固定小数点で評価して10進数で出力します
- 今回のシミュレーター上は「点の位置(何個左にズラすか)」を変えられるようになっています(実際の固定小数点は決め打ちであり、変えられません)
- 点位置をマイナスにすると、点が右にズレていきます
- 点がズレることで、各桁を2の何乗で評価するかがズレていくことを確認しましょう!
固定小数点シミュレーターの考察
点の位置を移動すれば、細かい小数も表現できる!
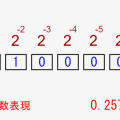
↑の例では、3.5と大きめの小数の値を例にしていましたが、↓のように点の位置を大きくずらすと、「0.2578125」といったように、細かい小数も表現可能になります!

固定小数点だと表現できる数の範囲が限られる!
↑の例もそうですが、小数点が固定だと表現できる数が限られます。↑の例だと整数部分が1bitしかなく、0 or 1しか表現できません!ほぼ整数を表すのは不可能になってしまうんです><
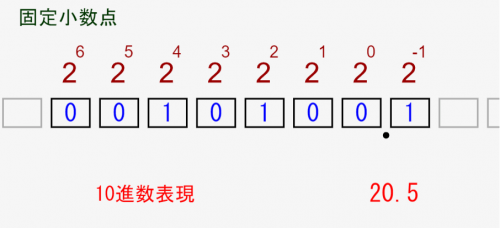
逆に、整数部分を多く取ろうと↓のようにすると、小数点以下は0.5のみしか表現できなくなります。これではまずいですよね。
この固定小数点の問題を回避するために、次回説明する「浮動小数点」を一般的には使用します!
まとめ:「固定小数点 = 小数点を一定数ずらして、小数も表現可能にした方式」
今回説明したように、固定小数点方式はすごく簡単で、「小数点を一定数ずらして、小数も表現可能にした方式」です。例えば、4つずらすと決めて、それ以下のbitは2進数の小数として評価するように決めるんです。
2進数の小数は↓のように2の累乗の逆数で評価します。
2桁目: \(\large{2^{-2} = \frac{1}{4}}\)
3桁目: \(\large{2^{-3} = \frac{1}{8}}\)
ただ、上記のように、小数点のズラす位置を固定で決めるため「整数部分が足りない」「小数部分が足りない」といったことが起こります。
そのため次回記事で説明する浮動小数点方式が必要になるわけです!
- 「固定小数点 = 小数点を一定数ずらして、小数も表現可能にした方式」
- 小数点部分は2の累乗の逆数として評価する
⇒「データ型」カテゴリ記事一覧
その他関連カテゴリ