「2の補数表現(負の数の表現)」をシミュレーションで解説！[コンピューターの原理基礎]

2022-02-27　

コンピューターは2進数の世界で動いています。2進数は1001101101みたいな感じで0と1の羅列になります。

前回は「1の補数表現」での負の数の表し方を説明しました。今回はそれを改変した「2の補数表現」での負の数の表現について解説します！

おさらい：「1の補数表現 = 全bit逆転させて負の数を表す」

絶対値表現では先頭bitを1にする形で負の数に変換しましたが、1の補数表現では↓のような取り方をします。

1の補数表現 = 正の数のbitを全部逆転させる(1⇔0)

非常に単純なルールで↓のような対応関係になります（1バイト表現）

1 ⇒ 0001、 -1 ⇒ 1110
2 ⇒ 0010、 -2 ⇒ 1101
3 ⇒ 0011、 -3 ⇒ 1100

絶対値表現とは全く違う変換ですが、「負の数＝先頭bitが1」というのは共通しています

これは絶対値表現でもあった問題です。

↓のように「1111＝-0」という謎の数が出現します。

00000 ⇒ 0、1111 ⇒ -0

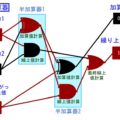
それゆえに、↓のように正数と負数を足した時、おかしくなる場合がでてきます。このパターンだと、オーバーフローを起こして、2+(-1)=0となってしまうんです。そのため、この場合補正が必要になります。

0010(+2) + 1110(-1)
↓普通に2進数加算
0000 （オーバーフローして0に）

これは、↓のように並べてみると一目瞭然です。
「-0」という謎の数があるからこそ、足し算の邪魔になっているんです！

3 ⇒ 0011
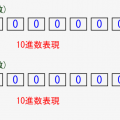
2 ⇒ 0010
1 ⇒ 0001
0 ⇒ 0000
-0 ⇒ 1111　（邪魔）
-1 ⇒ 1110
-2 ⇒ 1101
-3 ⇒ 1100

そこで、1の補数表現の問題点を簡単に解決するために、「1の補数表現に＋1する」ことを考えます。

すると、↓のように「-0」が消えて、キレイに2進数の順番に並ぶんです！

3 ⇒ 0011
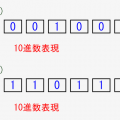
2 ⇒ 0010
1 ⇒ 0001
0 ⇒ 0000
-1 ⇒ 1111
-2 ⇒ 1110
-3 ⇒ 1101

また、10000000は10000001(-127)より一つ下の数ということで、-128として扱ることになります！「+0」と「-0」の重複がなくなり、全ての数が有効活用できるわけです！（1の補数や絶対値表現では-128は表現できません）

-1から0になるとこで、1111⇒0000に逆転していますが、、、、1足して10000になったと見なせば問題ないんです！（このように上の桁に溢れることをオーバーフローと呼びます）

実際に1バイト(8bit)で「1の補数表現(負の数の表現)」がどうなるか、シミュレーターで確認してみましょう！

シミュレーターの説明

絶対値

↑で正数と負数の比較をしますが、こちらのシミュレーターでは負数～正数で2進数として連続になることを改めて確認しましょう！

シミュレーターの説明

10進数

今回はコンピューターで負の数を表す方法の一つ、2の補数表現について説明しました。2の補数は1の補数で、「-0」があった部分を消すために＋1して補正したものです。

こうすることで、正数も負数も関係なく、2進数として連続になり、加算演算が可能になるんです！やや定義がややこしいですが、計算機での演算が楽になるため「2の補数による表現」が負の数を表す方式として一般的になっています。
　

まとめ

[関連記事] コンピューターでの負の数の表し方

3．2の補数表現(本記事)