コンピューターの原理基礎:足し算を行う基本論理回路をシミュレーターで理解しよう![半加算器/全加算器での1桁2進数計算]
前回の記事で、計算回路の説明の前段階として、2進数とは何かを説明させて頂きました。結論としては、「10進数との違いはいつ繰り上がるかのルールが違うだけ(2になった時点で繰り上がってしまう)」です。そしてその特徴は「10進数よりも1桁単位の計算パターンが非常に単純になる」にありました。1桁当たりの状態としては「0か、1か、それとも繰り上がりか」の3つしかないんです。
今回はその「0/1/繰り上がり」の3つの場合を計算できる、足し算計算機(加算器)をどうやったら基本回路で実現できるのかを説明します!単純な回路の組み合わせが、人間よりも素早く計算できる高度なマシンとなるのです!
![コンピューターの原理基礎:足し算を行う基本論理回路をシミュレーターで理解しよう![半加算器/全加算器での1桁2進数計算]](https://retu27.com/wp-content/uploads/rapture_20170820131037-500x380.jpg)
目次
2進数の足し算
まず2進数の足し算のパターンを理解するために、例題として下記の2進数の足し算を行う場合を考えます。(1つ目の数字を青色、2つ目の数字を赤色で以後示していきます)
1101 + 1110 = ?
この計算についても、10進数と同じように下の位から計算していけばいいのです。下記のように順番の計算していきます。
2の位: 0 + 1= 1
さて、ここで3の位を計算すると問題が発生します。足し算をすると2となり、前回記事で説明した「繰り上がり」が発生するのです。
この場合は前回の記事と同様に。「3の位は0とし、4の位に1繰り上がり」という扱いをします。
となると4の位は大変です。実は繰り上がってきた値も含めた3つの数字の足し算を行わなければならないのです。
そうすると実は「3」という大きな数がでてくるのです!でも、3は2進数でいう「11」なので、下記のようにあらわせます。
このように多少複雑なパターンがありますが、1つ目の数字(青色)と2つ目の数字(赤色)と繰り上がり数字(紫色)の3つの数字の足し算を各桁で行えば、2進数の計算式は簡単に作れるのです。
繰り上がってきた値を考慮しない、2つの数の加算(半加算器)
それでは各桁の計算を行う回路を考えていきます。上記の4桁目の繰り上がってきた数がある場合を考えると3つの数となりややこしいので、まずは繰り上がりがない場合を考えます(これを半加算器と呼びます)。そうすると、入力1(1つ目の数字)と入力2(2つ目の数字)の1桁の足し算は下記のパターン表で表せます。
| 入力1 | 入力2 | 加算値 | 繰り上がり値 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
加算値とは「合計値、ただし繰り上がりがあった場合はその分を差っ引いた値」を示しています。つまり、「繰り上がりを考慮した、その桁の最終的な加算結果」です。この上記の4つのパターンを回路で表せれば、2進数の各桁の計算は表現できます。それでは、1)繰り上がり値と2)加算値のそれぞれの計算方法を考えていきます。
1)繰り上がり値の計算
まず簡単な繰り上がり値の計算から説明します。繰り上がり値の計算パターンは下記のとおりです。
| 入力1 | 入力2 | 繰り上がり値 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
これってどこかで見たことないですか?繰り上がりがおこるのは、入力1と入力2がともに1のときのみ…。そうです。以前の記事で説明したAND回路と全く同じパターンなんです!なので、下記のシミュレーターのAND回路で実現できてしまうのです!
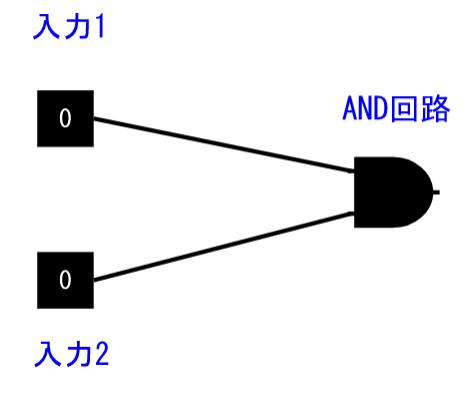
このAND回路だけで繰り上がり値の計算は完了です。
2)加算値の計算
それでは次に加算値についてです。加算値のパターンは下記のとおりです。
| 入力1 | 入力2 | 加算値 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
簡単にいうと「入力1と入力2のどちらか1つのみが1の場合に1を出力」するパターンです。このような、どちらか一方のみ1のとき、1となるものをXOR回路と呼びます。ちょっとOR回路に似ていますよね。OR回路との違いは「入力1と入力2がともに1のとき0となる」ことだけです。ですので、下記のOR回路をうまく使うと、この計算は実現できそうです。
このOR回路を基本とし、「入力1と入力2がともに1のときは0とする」ように改変出来ればです。入力1と入力2がともに1…これって上で説明した「AND回路」の動きですよね!そして、この「AND回路が1のときは、強制的にOR回路の出力を0にする」ことができればこの回路が実現できます。パターンでいうと下記のとおり。
| OR回路出力 | AND回路出力 | 加算値 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
上記のパターンから「OR回路が1、AND回路が0のときにのみ1を出力するようにする」ことができればいいことがわかりました。
ここで、1つの閃き。AND回路の値を反転すれば、「OR回路が1、AND回路反転値が1のときにのみ1を出力するようにする」とすると言い換えられます。この統合はAND回路で実現できますよね。パターン表でみてみましょう!
| OR回路出力 | AND回路後に NOT回路(反転) |
加算値 |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
このパターン、AND回路の出力そのものです。ですので、↓のような「OR回路」と「AND回路後にNOT回路を通した値」をAND回路で統合すれば、目的の値が出てきます。
↓のシミュレーターでは、入力1と入力2をタップで変化させられます。入力を変更して、計算過程と出力が変わることを確かめてください!
[加算値計算回路(XOR回路)]
「入力1と入力2のどちらか1つのみが1の場合に1を出力」ですよね!これを単純化して「XOR回路」と呼び、下記のような記号であらわします。

「繰り上がり値」も出力する半加算器シミュレーター
上記のようにXOR回路ができあがると、半加算器は下記のような単純な回路で表現できます。加算値は↓のようにXOR回路、繰り上がり値はAND回路で計算できてしまうんです!
- 入力部分をタップすると、0と1を切り替えられます
- 入力を切り替えて、半加算器として「加算値」「繰り上がり値」が正常に出力されているか確認してみましょう!
繰り上がってきた値を考慮した全加算器
それでは、今度は繰り上がってきた値を考慮した全加算器を考えます。今回は下記のように、入力1と入力2とく上がり値の3つの値の計算となります。
でもこれって下記のように2つの数の足し算の組み合わせで表せるのです。3つの数の足し算は、2つの数の足し算を2回やれば表現できるからです。
(入力12加算値 + 繰り上がってきた値) = 最終加算値 #(繰り上げ値2)
つまり、上記の半加算器を2つ組み合わせれば全加算器は実現できてしまいます!しかし、繰り上げ値の考慮に注意が必要です。上記のように、足し算を2回行うので、2つの繰り上げ値が出力される事になります。これをどう扱えば良いか。
答えは、繰り上げがあるパターンを考えてみると簡単です。
つまり、「繰り上がり値1が1 && 繰り上がり値2がともに1」という面倒な場合はないのです。ですので最終繰り上がり値は下記のパターンであらわせます。
| 繰り上がり値1 | 繰り上がり値2 | 最終繰り上がり値 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 起こりえない! |
一番下のパターンは起こりえないので、上3つのパターンをみたした回路で実現できます。このパターンは、OR回路でですよね!ということで全加算器の最終的な回路は↓のシミュレーターの形のなります!
全加算器シミュレーター
- 入力と繰り上がってきた値部分をタップすると、0と1を切り替えられます
- 入力と繰り上がってきた値を変更して、色々と値をかえて試してみてください!
水色の枠で示しているのが、上記で説明してきた半加算器です。半加算器を2つ使って、3つの数(入力1と入力2と繰り上がってきた値)の足し算をしているわけです。これ、実は左の3つの入力内の、1の数をカウントしているだけでもあります(繰り上がり値も入力3とみなす)
| 3つの入力のうち、 1の数 |
繰り上がり値 | 加算値 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 1 | 0 |
| 3 | 1 | 1 |
上記のシミュレーターの入力3つをいろいろ変えてみると、↑のパターン通りの動きをするのがわかります。そして、上記の表の繰り上がり値を2桁目、加算値を1桁目として2進数をみると、見事に入力の1の数をカウントしているのが分かると思います。(0⇒00、1⇒01,2⇒10、3⇒11という対応関係になってます)
だから、「全加算器=3つの入力を受け取って、その足した数を[加算値][繰り上がり値]の2つの出力で表す回路」とも言えるわけです。
この全加算器を組み合わせることで、どんなに長い数でも足し算ができるようになるんです!ここについては、次回シミュレーターを交えて説明します!
まとめ:どんなに複雑な計算も、AND回路/OR回路/NOT回路で表現できる!
上記のように色々と回路を交えて説明しましたが、すべてAND回路/OR回路/NOT回路で構成できているのが分かりますよね。XOR回路も途中ででてきましたが、それも上で示したように、3回路の組み合わせで実現できるので、加算器全てが3回路の組み合わせで構成できるということなんです!
ということで、次回はこの半加算器/全加算器を用いて実際の長い桁の足し算をしてみます!!
- 1桁の演算は、加算値はXOR回路、繰り上がり値はAND回路で実現できる。これを半加算器という
- 実際は、下の位から「繰り上がり値」がくるため、それを考慮する必要あり
- そのために半加算器を2つ組み合わせた「全加算器」を1桁の計算に用いる
⇒「CPU」カテゴリ記事一覧
その他関連カテゴリ









[…] コンピューターの原理基礎:足し算を行う基本論理回路をシミュレーターで理解しよう![半加算器/全加算器での1桁2進数計算]retu27.com […]