「1の補数表現(負の数の表現)」をシミュレーションで解説![コンピューターの原理基礎]
コンピューターは2進数の世界で動いています。2進数は1001101101みたいな感じで0と1の羅列になります。
前回は絶対値表現での負の数の表し方を説明しましたが、今回は「1の補数表現」での負の数の表現について解説します!
![「1の補数表現(負の数の表現)」をシミュレーションで解説![コンピューターの原理基礎]](https://retu27.com/wp-content/uploads/20220227190333-500x264.png)
目次
おさらい:「絶対値表現 負の数 = 先頭bidを1」にする!
コンピューターでは簡単に、「先頭のbitを1」という方法で負の数を表します。この中でも絶対値表現は単純で↓のようなルールで負の数を表します。
非常に単純なルールで↓のような対応関係になります(1バイト表現)
2 ⇒ 0010、 -2 ⇒ 1010
3 ⇒ 0011、 -3 ⇒ 1011
「1の補数表現 = 全bit逆転させて負の数を表す」
絶対値表現では先頭bitを1にする形で負の数に変換しましたが、1の補数表現では↓のような取り方をします。
非常に単純なルールで↓のような対応関係になります(1バイト表現)
2 ⇒ 0010、 -2 ⇒ 1101
3 ⇒ 0011、 -3 ⇒ 1100
絶対値表現とは全く違う変換ですが、「負の数=先頭bitが1」というのは共通しています
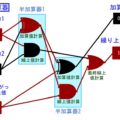
1の補数表現のメリット:加算の演算回路がそのまま使える
1の補数表現のほうが、絶対値表現より良い点があります。それはコチラの記事で書いている加算演算回路がそのまま使えるという点です。
例えば -3 ⇒ -2 ⇒ -1 と1つずつプラスしていく場合を見てみると↓のようになります。
1100 ⇒ 1101 ⇒ 1110
これは通常の論理的な足し算(2進数の足し算)と同じであり、マイナスであっても加算回路演算可能なことを意味しています!絶対値表現の場合はこのようになりません。
1の補数表現の問題点:「-0」があり、正の数と負の数の演算に修正が必要
これは絶対値表現でもあった問題です。
↓のように「1111=-0」という謎の数が出現します。
それゆえに、↓のように正数と負数を足した時、おかしくなる場合がでてきます。このパターンだと、オーバーフローを起こして、2+(-1)=0となってしまうんです。そのため、この場合補正が必要になります。
↓普通に2進数加算
0000 (オーバーフローして0に)
このような補正が大変なので、、、次の記事で説明する「2の補数表現」を使うことが多いです。
「1の補数表現(負の数の表現)」をシミュレーターで確認してみよう!
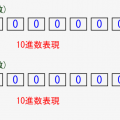
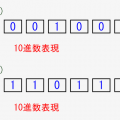
実際に1バイト(8bit)で「1の補数表現(負の数の表現)」がどうなるか、シミュレーターで確認してみましょう!
- 指定した絶対値(10進数)の正数と負数両方をbitで出力します
- 正数と負数が、真逆になっていることを確認しましょう
- 負の数は先頭bitが1であることも確認してみましょう
まとめ:「1の補数表現の負の数 = 全bitを逆転(1⇔0)」
今回はコンピューターで負の数を表す方法の一つ、1の補数表現について説明しました。絶対値表現と比べて加算回路が負数でも使えるというメリットがありますが、「-0」という謎の数が生まれ、正の数と負の数の足し算で問題になる場合がでてきます。
この問題を解決した「2の補数表現」を次回記事では説明していきます!
- 「1の補数表現の負の数 = 全bitを逆転(1⇔0)」
- 加算回路が使えるなどのメリットがあるが、一部計算で問題があり、特別処置が必要
⇒「データ型」カテゴリ記事一覧
その他関連カテゴリ