「2進数の絶対値表現(負の数の表現)」をシミュレーションで解説！[コンピューターの原理基礎]

2022-02-27　

コンピューターは2進数の世界で動いています。2進数は1001101101みたいな感じで0と1の羅列になります。

前回まで整数型の数値の表現方法を解説してきましたが、今回は負の数の表現方法の一つ「絶対値表現」について解説します！

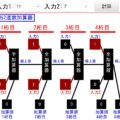
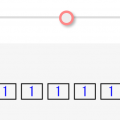
おさらい：「1バイト = 2進数8桁」

1バイト(1byte)は↓のように8つの箱(ビット)を組み合わせたデータになります。

8個の箱を組み合わせて、表せる数は\(２^8 = 256\)種類になります。0~255までの数ですね。
1ビットがデータの最小単位ではりますが、基本的にはこの1バイトを基本単位としてコンピューターのメモリサイズやストレージサイズは表されます！

前回までのシミュレーターでは、全て0と正の数のみ対象としてきました。しかし、実際には負の数も扱う必要があります。

コンピューターでは簡単に、「先頭のbitを1」という方法で負の数を表します。この中でも絶対値表現は単純で↓のようなルールで負の数を表します。

絶対値表現 = 正の数の先頭bitを1にしたもの = 負の数

非常に単純なルールで↓のような対応関係になります（1バイト表現）

1 ⇒ 0001、 -1 ⇒ 1001
2 ⇒ 0010、 -2 ⇒ 1010
3 ⇒ 0011、 -3 ⇒ 1011

これは仕方ないことです。↑の例のとおり、先頭bitを符号として使っているため、1バイトの数値として表せるのは最大で\(2^7=128\)になります。0もあるので－127～127までが絶対値表現で表せる範囲になります。

0は0000という表現になります。これについても先頭符号を1にできるので1000というbit配列が作れます。これは意味合いでいうと「-0」です。しかし、そんな数は必要ないので無駄になってしまいます。また、0が二パターンできるので、複雑になります。

0000 ⇒ 0、1000 ⇒ -0

こういった理由(+α)から、実際にコンピューターでつかわれるのは次回解説する「2の補数表現」になるかと思います。

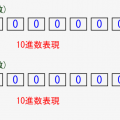
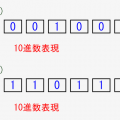
実際に1バイト(8bit)で負の数の表現がどうなるか、シミュレーターで確認してみましょう！

シミュレーターの説明

絶対値

↑で説明した通り、「-0」という謎の数が出てしまうことが分かると思います！

今回はコンピューターで負の数を表す方法について説明しました。今回説明した絶対値表現が一番単純で分かりやすいですが、「-0」という謎の数が生まれるなどの問題があります。

また「演算がしにくい」というような問題もあります！そこは次回記事で説明していきます！
　

まとめ

[関連記事] コンピューターでの負の数の表し方

1．絶対値表現(本記事)